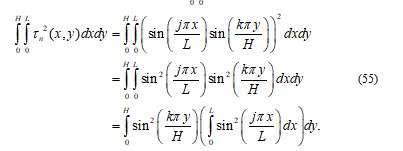Penerapan Fungsi Green dari Persamaan Poisson pada Elektrostatika
Main Article Content
Abstract
The Dirac delta function is a function that mathematically does not meet the criteria as a function, this is because the function has an infinite value at a point. However, in physics the Dirac Delta function is an important construction, one of which is in constructing the Green function. This research constructs the Green function by utilizing the Dirac Delta function and Green identity. Furthermore, the construction is directed at the Green function of the Poisson's equation which is equipped with the Dirichlet boundary condition. After the form of the Green function solution from the Poisson's equation is obtained, the Green function is determined by means of the expansion of the eigen functions in the Poisson's equation. These results are used to analyze the application of the Poisson equation in electrostatic.
Article Details
Section
How to Cite
References
A. Kleshchev, “Green’s functions method in problems of sound diffraction,” American Journal of Modern Physics, vol. 6, no. 4, pp. 56-65, 2017, [Online], doi: 10.11648/j.ajmp.20170604.13.
K. A. Shah, Mathematical modeling of malignant skin tumor in human body, Thesis, Dept. Math., Veer Narmad South Gujarat University, Surat, India, 2015.
W. H. Hayt & J. A. Buck, Engineering Electromagnetics, Singapore: McGraw-Hill Higher Education, 2006.
R. L. Herman, Introduction to Partial Differential Equations, North Carolina, NC, USA: R.L Herman, 2015.
M. Humi and W. B. Miller, Boundary Value Problem and Partial Differential Equations, Boston, MA, USA: Pws. Pub. Co., 1991.
M. Malik, Fungsi Green untuk Persamaan Poisson, Skripsi, Program Studi Matematika, Universitas Indonesia, Depok, 2009.
M. Munaqqib, “Penyelesaian masalah syarat batas persamaan Helmhotz menggunakan dual reciprocity boundary element method,” Jurnal Logika, vol. 8, no. 2, pp. 115-132, 2018.
K. A. E. A. A. Elnour, “On the calculus of Dirac delta function with some applications,” International Journal of Mathematics Trends and Technology (IJMTT), vol. 56, no. 4, pp. 258-259, 2018, doi: 10.14445/22315373/IJMTT-V56P537.
A. Royston, Notes on the Dirac Delta and Green Functions, Chicago, IL, USA: University of Chicago, 2008.
K.T. Tang, Metode Matematika untuk Sains dan Teknik 2, New York, NY: Springer, 2007.